VECTORES CARTESIANOS EN 3 “D” ⚙️ Vectores de Posición ⚙️ Producto Punto ⚙️

 

Aquí ya se debe de saber interpretar los elementos en 3 "D" no solo vectores, sino cuerdas, tubos, etc. Para ello debe tener un buen análisis. 

Si deseas la explicación en YouTube click a la imagen 👆👆👆

📝 Si deseas asesoría personalizada; explicación de ejercicios. Contáctame

TEMARIO

• Vectores Cartesianos en 3 "D"
• Vectores de Posición
• Producto Punto

¿Cuáles son las operaciones vectoriales cartesianas en 3 D ? 

Las operaciones de álgebra vectorial, cuando se aplican a la resolución de problemas en tres dimensiones, se simplifican considerablemente si primero se representan los vectores en forma vectorial cartesiana. En esta sección presentaremos un método para hacer esto.

 

Sistema coordenado derecho

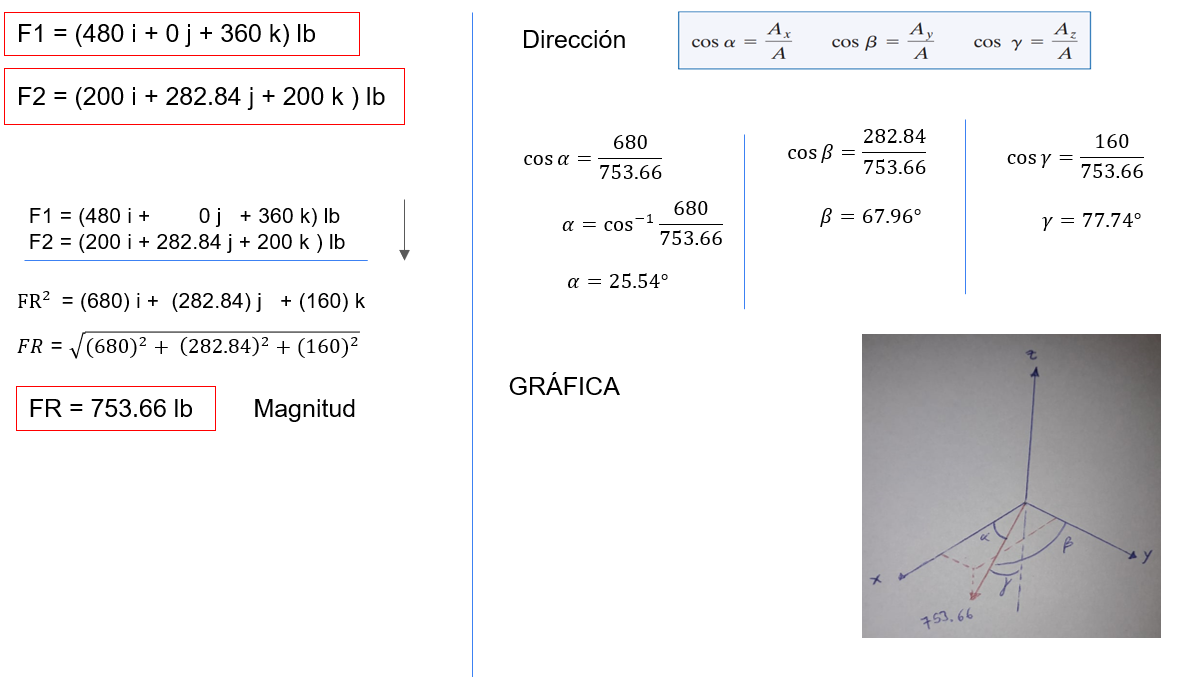
En la imagen se muestra el vector A en 3 D, descompuesto en sus coordenadas x,y,z de esa manera se expresa el vector en su forma vectorial.

 

Representación de un Vector Cartesiano

Se determina la descomposición de un vector en 3 D. en sus coordenadas correspondientes.

Magnitud de un Vector cartesiano

Se determina usando la formula de Pitágoras "raíz cuadrada de todos los valores elevados al cuadrado" los valores son el vector expresado en sus componentes x,y,z, "vector cartesiano" 

Dirección de un vector cartesiano

Para el cálculo de las dirección se aplica la formula dada en la imagen en la cual relaciona el ángulo con respecto al eje de coordenada de cada punto. 

• Alfa es el ángulo que forma el vector A con respecto a la coordenada x, es por ello que la formula relaciona alfa con Ax.

• Beta es el ángulo que forma el vector A con respecto a la coordenada y, es por ello que la formula relaciona alfa con Ay. 

• Gamma es el ángulo que forma el vector A con respecto a la coordenada z, es por ello que la formula relaciona alfa con Az. 

Cuadro elaborado para observar la relación de cada eje de coordenada (x,y,z) con el ángulo (alfa, beta, gama) y la simbología ( i,j,k)

Vector Unitario

Viene a determinarse el vector expresado de manera vectorial dividido entre la magnitud lo que representa a la distancia de un punto hacia otro. 

En algunos ejemplos desarrollados la magnitud del vector es la distancia de una cuerda dada. 

Ejemplo del Libro de Hibbeler Estática 12va edición

Hasta aquí culmina la explicación de los ejercicios desarrollados con el tema de descomposición de un vector en 3 D  a sus ejes coordenados (x,y,z) asimismo como determinar la magnitud, el vector unitario del vector. 

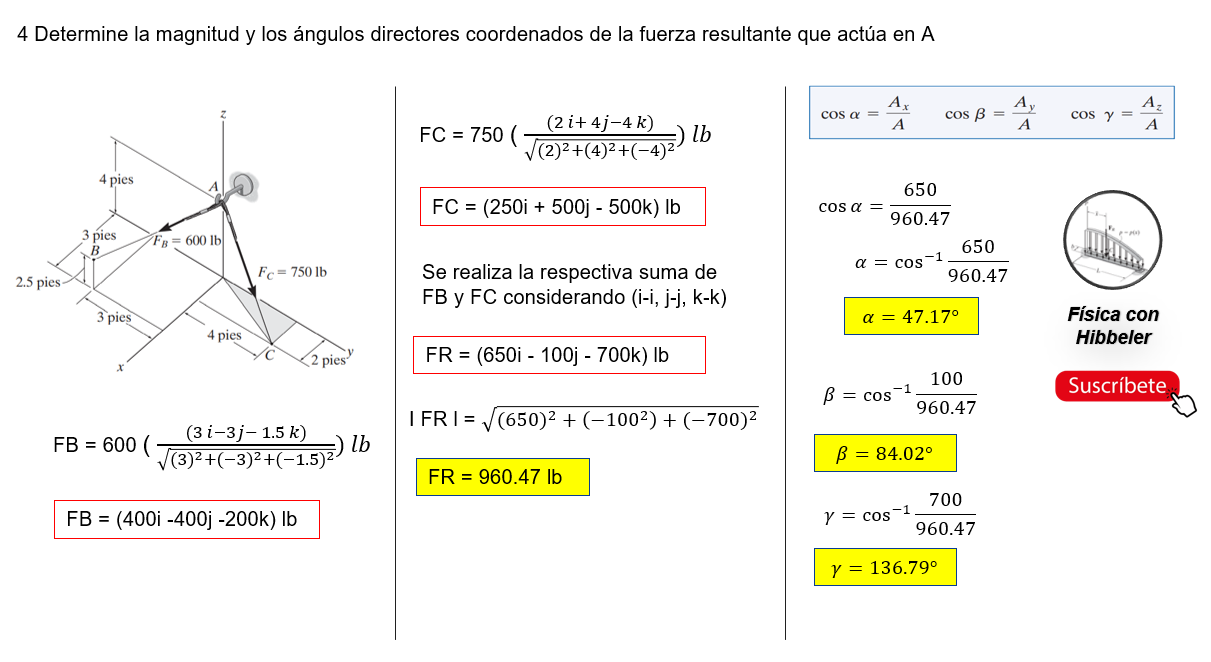
Vector Posición 

Un vector de posición r se define como un vector fijo que ubica un punto en el espacio en relación con otro punto. Por ejemplo, si r se extiende desde el origen de coordenadas, O, hasta el punto P(x, y, z),

Con mucha frecuencia, en problemas tridimensionales de estática, la dirección de una fuerza se especifica por dos puntos a través de los cuales pasa su línea de acción. Tal situación se muestra en la figura 2-38, donde la fuerza F está dirigida a lo largo de la cuerda AB. Podemos formular F como un vector cartesiano al observar que esta fuerza tiene la misma dirección y sentido que el vector de posición r dirigido desde el punto A hasta el punto B sobre la cuerda. Esta dirección común se especifica mediante el vector unitario u  r>r. Por lo tanto

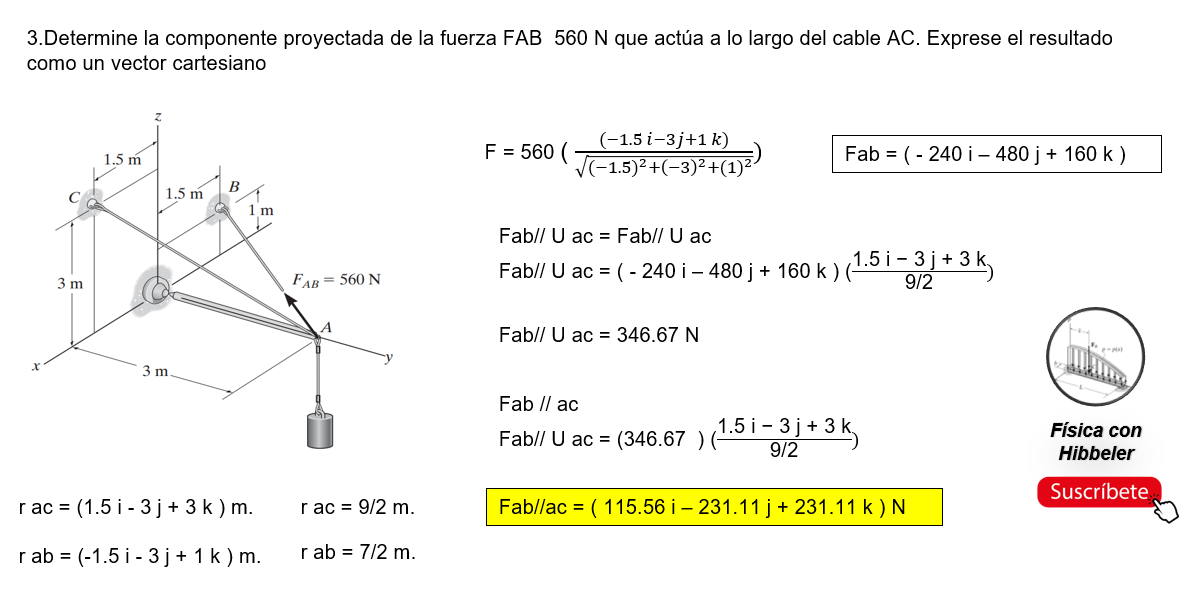
Producto punto

Algunas veces, en estática debemos localizar el ángulo entre dos líneas o las componentes de una fuerza paralela y perpendicular a una línea. En dos dimensiones, esos problemas pueden resolverse por trigonometría puesto que las relaciones geométricas son fáciles de visualizar. Sin embargo, en tres dimensiones esto suele ser difícil, y en consecuencia deben emplearse métodos vectoriales para encontrar la solución. El producto punto define un método particular para “multiplicar” dos vectores y se usa para resolver los problemas antes mencionados. El producto punto de los vectores A y B, que se escribe A.B, y se lee “A punto B”, se define como el producto de las magnitudes de A y B y el coseno del ángulo u entre sus colas.

📝 Si deseas asesoría personalizada; explicación de ejercicios. Contáctame

Eso es todo lo que respecta al tema de vectores cartesianos en 3 D, vectores de posición, producto punto.
Este contenido fue realizado con la intención de contribuir al estudio con lo que respecta a la base de la ingeniería. Te invito a brindar tu opinión.